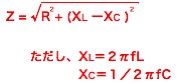インピーダンス（１）〜御隠居の電気基礎

９. インピーダンス（１）

交流回路における電流の流れにくさを表すものにリアクタンスがあることを前回勉強した。そのリアクタンス以外にインピーダンスと呼ばれるものも電流の流れにくさを表す場合に使われる。

負荷が抵抗のみで構成されている回路: 負荷が抵抗のみで構成されている場合は、直流回路と同様に抵抗成分が回路全体の電流の流れにくさを表し、単に「抵抗」と呼び、単位はオーム［Ω］を用いる。
負荷がコイルとコンデンサの組み合わせで構成されている回路: 負荷がコイルとコンデンサの組み合わせで構成されている場合は、コイルの電流の流れにくさを誘導リアクタンス、コンデンサの電流の流れにくさを容量リアクタンスと呼び、負荷全体の電流の流れにくさは、それぞれのリアクタンスを合成したもので、単に「リアクタンス」と呼ぶ。単位はオーム［Ω］を用いる。
負荷が抵抗、コイル、コンデンサの組み合わせで構成されている回路: 負荷が抵抗、コイル、コンデンサの組み合わせで構成されている場合、負荷全体の電流の流れにくさは、抵抗とリアクタンスを合成したもので、これを「インピーダンス」と呼ぶ。単位はオーム［Ω］を用いる。

R-L直列回路

抵抗（R[Ω]）とコイル（L[H]）が直列接続された交流回路を考えてみる。

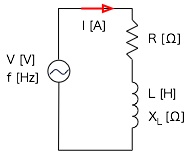
直列回路の場合、抵抗、コイルを流れる電流値は全体を流れる電流値I[A]に等しい。このとき、抵抗部分の電圧をV_R、コイル部分の電圧をV_Lとすると、それぞれの電圧は、次のように表せる。

ＶR ＝ Ｉ・Ｒ
ＶL ＝ Ｉ・ＸL

　ただし、ＸL＝２πｆＬ

ここで注意しなければならないのは、位相である。抵抗部分の電圧と電流は同位相であるが、コイル部分の位相は、電流が電圧より90度（π／２）遅れている。ここで直列回路の場合、電流を基準に考えると次のような関係になる。

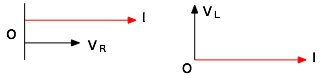
つまり、抵抗とコイルで位相が異なるので、ベクトルで考える必要があるわけだ。ということで、２つの電圧の合成電圧、すなわち、V[V]は次のようになる。

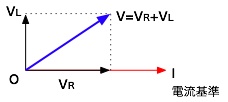
これを三平方の定理で考えると、

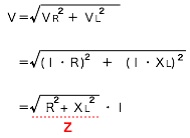
となります。このときＺの部分が電流を妨げる部分でインピーダンスということになります。つまり、R−L直列回路のインピーダンスは次式で計算できることになります。

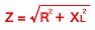
R-C直列回路

抵抗（R[Ω]）とコンデンサ（C[F]）が直列接続された交流回路を考えてみる。

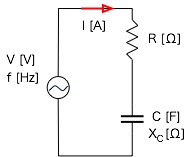
コンデンサ部分の位相は、電流が電圧より90度（π／２）進んでいる。ここでR−L直列回路と同様に考えると次のような関係になる。

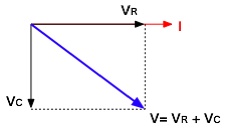
そこでR−L直列回路と同様に、三平方の定理で考えると、R−C直列回路のインピーダンスは次式で計算できることになります。

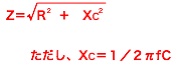
R-L-C直列回路

抵抗（R[Ω]）とコイル（L[H]）、コンデンサ（C[F]）が直列接続された交流回路を考えてみる。

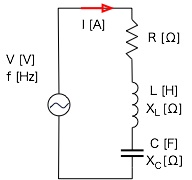
この場合もこれまでと同様に考えればよいが、コイル部分の位相は、電流が電圧より90度（π／２）遅れ、コンデンサ部分の位相は、電流が電圧より90度（π／２）進んでいる。つまり、誘導リアクタンスと容量リアクタンスの向きが正反対であり、その差が合成リアクタンスになることになる。このことからR-L-C直列回路は次のような関係になる。

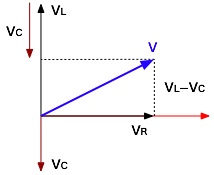
そこでR-L-C直列回路もこれまでと同様に、三平方の定理で考えると、R-L-C直列回路のインピーダンスは次式で計算できることになります。

先頭に戻る