5. 交流の性質
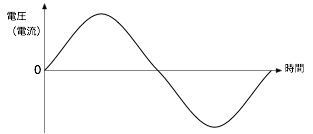
直流は時間経過とともに電圧、電流が常に一定でした。一方、 電圧、電流の大きさと方向が時間経過とともに周期的変化するものを交流(正弦波交流)と呼びます。 ここでは、正弦波交流の電圧を中心に勉強しますが、電流も同じように考えることができます。
周波数
正弦波交流は、同じ波形を繰り返します。この1回の変化に要する時間を周期と呼びます。 そして1秒間に変化する回数を周波数と呼び、単は[Hz](ヘルツ)を使います。
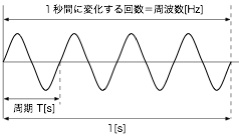
周期Tと周波数fには、逆数の関係があります。
T [s] = 1/f 周期=1/周波数 f [Hz] = 1/T 周波数=1/周期
最大値と瞬時値
交流における最大値は電圧Vmも電流Imも波形の頂上部分になります。
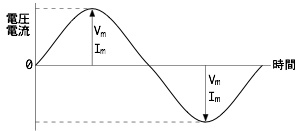
また、交流は時間経過とともに電圧、電流の大きさが変化します。 そのため、ある時間における瞬間の電圧、電流を瞬時値と呼びます。
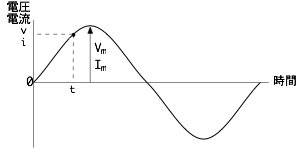
ある時間tにおける電圧、電流の瞬時値v、iと、その最大値Vm、Imの間には以下の関係があります。
v = Vm・sinωt i = Im・sinωt
このときω(オメガと読む)をのことを角速度といい、 単位[rad/s](ラジアン/秒)で表します。角速度は、正弦波形の1秒間に変化する角度を表すもので、 周波数と関係があります。例えば、1秒間に1周期だけ変化すれば、その角度は2πラジアンになります。 つまり、角速度と周波数の間には、次の式が成り立ちます。
ω [rad/s] = 2πf
位相差
下の図では3種類の電圧を表していますが、それぞれ波形がずれています。 この波形のズレは角度で表され、それを位相差と呼びます。
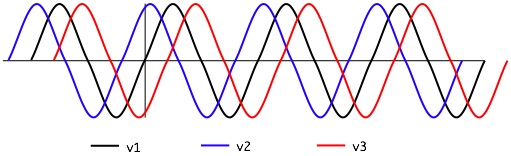
いまv1を基準にし、v1とv2の位相差がθ1(θはシータと読みます)、v1とv3の位相差がθ2だとします。 この3種類の電圧の瞬時値を式で表すと次のようになります。 なお、各電圧の最大値はそれぞれVm1、Vm2、Vm3とします。
v1 = Vm1・sinωt v2 = Vm2・sin(ωt + θ1) v3 = Vm3・sin(ωt - θ2)
ここではv1を基準にしているので、それぞれv2はv1よりθ1だけ位相が進んでいると言い、 v3はv1よりθ2だけ位相が遅れていると言います。
平均値
反周期(T/2)について平均した値を交流の平均値と呼びます。 平均値を表す記号には、一般に電圧はVa、電流はIaを使います。 そして、平均値はそれぞれの最大値を2/π(≒0.637)倍した値になります。
平均値 = (2/π)・最大値≒0.637・最大値
Va = (2/π)・Vm ≒ 0.637Vm Ia = (2/π)・Im ≒ 0.637Im
実効値
交流の電圧、電流を、これと同じ仕事をする大きさで表したものを実効値と呼びます。 通常、家庭で言う100[V]は、この実効値になります。 一般に電圧は記号V、電流はIで表します。 そして実効値は、それぞれの最大値を1/√2(≒0.707)倍した値になります。
実効値 = (1/√2)・最大値≒0.707・最大値
V = (1/√2)・Vm ≒ 0.707Vm I = (1/√2)・Im ≒ 0.707Im

