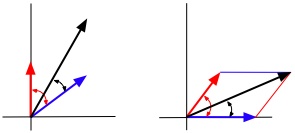
7. 交流とベクトル
これまでの勉強で、交流を正弦波で表現することやった。これによって時間変化に対して電圧や電流が変化することも分かった。 ここでは、その正弦波とベクトル(大きさと方向)の関係について勉強する。 ただ、ちょっとややこしい。まずは、基本的な式で考えてみよう。
交流の瞬時値 v = Vm・sin(ωt + θ)
ここで、位相差θを0として考えてみる。すると、ωtが0、90度(π/2ラジアン)、180度(πラジアン)、270度(3π/2ラジアン)、 360度(2πラジアン)のときを計算すると次のようになる。
wt = 0 のとき v = Vm・sin0 = 0 wt = 90度 のとき v = Vm・sin(π/2) = Vm wt = 180度 のとき v = Vm・sinπ = 0 wt = 270度 のとき v = Vm・sin(3π/2) = -Vm wt = 360度 のとき v = Vm・sin(2π) = 0
これを図示すると次のようになる。
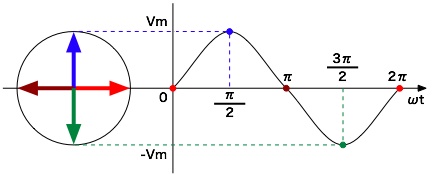
このとき左側の円に描いた矢印が、それぞれのベクトルになる。 この場合、大きさはすべて等しくVmであるが、方向は違う。このように大きさと方向で表現したものをベクトルと呼ぶ。
次に位相差のある2種類の正弦波において、その合成された正弦波について考えてみよう。 いま、青い正弦波を基準として、θだけ進んだ赤い正弦波との合成した正弦波を黒で表現している。 このとき合成後の黒い正弦波は青い正弦波よりφだけ進むと仮定する。
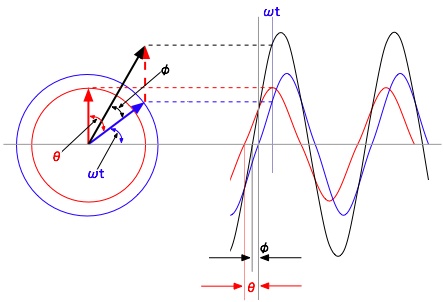
まず、任意のωtにおけるそれぞれのベクトル(回転ベクトルとも呼ぶ)を左側に示している。 このとき青と赤のベクトルをそれぞれ平行移動してできる平行四辺形の対角線が、 黒の正弦波のωtにおけるベクトルとなる。これをベクトルの和(ベクトル合成とも呼ぶ)という。
また、それぞれのベクトルはお互いの位置関係(位相関係)を保持したまま回転している。 そのため、任意の位置(どれかのベクトルを基準とすると理解しやすい)にベクトル群を固定させても、 お互いの位相関係は変化しない。このようなベクトルを静止ベクトルと呼ぶ。 なお、進み角は反時計回りに計り、遅れ角は時計回りに計った静止ベクトルで表現している。