御隠居の電気基礎

３. 練習してみよう（１）

練習１

図のような回路において、電流計の値は何アンペアになるか？

---

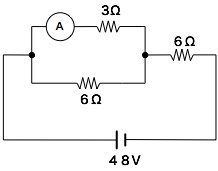
まず、最初に合成抵抗Rを求め、回路全体を流れる電流Iを計算する。

　並列部分を和分の積で求め、残りは直列接続なので、その総和を求める。

  R = {3・6/(3 + 6)} + 6 = 8 [Ω]

  オームの法則により電流を計算する。

  I = 48／8 = 6 [A]

次に並列部分の電流値は回路全体を流れる電流値に等しいから、
分流の式により電流計を流れる電流値を計算する。

  Ia = {6／(3 + 6)}・I
     = {6／(3 + 6)}・6 = 4 [A]

よって、答えは４［A］となる。

練習２

図のような回路において、電流計の値が ２アンペアのとき、電圧計の値は、 何ボルトになるか？

---

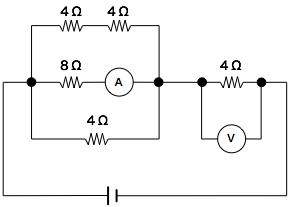
電流計の値が分かっているので、８［Ω］にかかる電圧（Va）を計算する。

  Va = 8・2 = 16 [V]

並列接続の抵抗には、電圧が等しく掛かるので、Vaを使って各電流値を計算する。

  上段  I1 = Va／(4 + 4) = 16／(4 + 4) = 2 [A]
  中段  I2 = 2 [A]
  下段  I3 = Va／4 = 16／4 = 4 [A]

並列部分全体にかかる電流は、各電流の総和になるので、

  I = I1 + I2 + I3 = 2 + 2 + 4 = 8 [A]

直列接続にかかる電流値は等しいので、Iを使って電圧を計算する。

  V = 4・I = 4・8 = 32 [V]
  
よって、答えは３２［V］となる。

練習３

図のような回路において、電圧計の値が０のとき、 抵抗Rは何オームになるか？

---

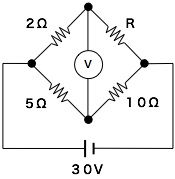
電圧計の値が０を指しているということは、２Ωの抵抗にかかる電圧V1と
５Ωにかかる電圧V3が等しく、また、RΩの抵抗にかかる電圧V2と１０Ω
にかかる電圧V4も等しくなるということだ。

  V1 = V3  または  V2 = V4
  
分圧の式によりV2とV4を計算する。

  V2 = {R／(2 + R)}・V
  V4 = {10／(5 + 10)}・V

ここで、V2 = V4 であるから、

  {R／(2 + R)}・V = {10／(5 + 10)}・V
  {R／(2 + R)}    = {10／(5 + 10)}
                R = (2 + R)・2／3
               3R = 4 + 2R
          3R - 2R = 4
                R = 4 [Ω]

よって、答えは４オームとなる。

---

上のような回路をブリッジ回路と呼ぶ。一般的な形は次のような回路図となる。

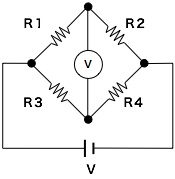
このとき電圧計（実際には、電流計、検流計でもよい）が０を指示する場合、 上記の問題と同じように考えてみる。

電圧計の値が０を指しているということは、抵抗R1にかかる電圧V1と
抵抗R3にかかる電圧V3が等しく、また、抵抗R2にかかる電圧V2と抵抗R4に
かかる電圧V4も等しくなる。

  V1 = V3  または  V2 = V4
  
分圧の式によりV2とV4を計算する。

  V2 = {R2／(R1 + R2)}・V
  V4 = {R4／(R3 + R4)}・V

ここで、V2 = V4 であるから、

  {R2／(R1 + R2)}・V = {R4／(R3 + R4)}・V
  {R2／(R1 + R2)}    = {R4／(R3 + R4)}
         R2(R3 + R4) = R4(R1 + R2)
         R2R3 + R2R4 = R1R4 + R2R4
         R2R3        = R1R4

つまり、対角上にある抵抗の積が等しくなるとき、 電圧計の値が０を指すことになる。これをブリッジ回路の平衡条件という。 これは大事な式なので覚えておく方が良い。

ブリッジ回路の平衡条件  R1R4 = R2R3

先頭に戻る