御隠居の電気基礎

２. オームの法則と合成抵抗

電圧、電流、抵抗の関係

電圧、電流、抵抗の関係を表した有名な法則がオームの法則です（中学校の理科で習うかな？）。 下のような図を書いて覚えた人もきっと多いのでは？

これは下のような回路図を考えた時、

電圧、電流、抵抗の関係を式で表すと次のようになります。これをオームの法則と呼んでいます。

V = R・I

この式を変形して、電流、抵抗を計算するオームの法則は次の式になります。

I = V／R
R = V／I

上の図で習った人は、これらの式を下のように考えればいいでしょう。

直列回路と直列接続

２つの抵抗を接続した回路を考える場合、下の図ような回路を直列回路と呼び、 このような抵抗の接続方法を直列接続と呼んでいます。

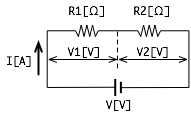
直列回路の特徴として、各抵抗に流れる電流は一定（同じ）で、電圧は各抵抗に分配されます。 これを分圧と言います。つまり、以下の関係式が成立します。

V = V1 + V2 ・・・(1)
V1= R1・I   ・・・(2)
V2= R2・I   ・・・(3)

次に上の回路図と等しくなるような下の図のような回路を考えます。これを等価回路と呼びます。

この等価回路のオームの法則と上の関係式を合わせて考えると、次のようになります。

V = R・I ・・・(4)

(2)、(3)、(4)式を(1)式に代入

R・I = R1・I + R2・I

両辺からIを消去して、

R = R1 + R2

このようにして求めたRを合成抵抗と呼びます。 また、直列接続の合成抵抗は、各抵抗値の総和になります。 すなわち、抵抗の数に関係なく、その総和が合成抵抗の値になります。

また、直列接続では、電流を考えることなく各抵抗にかかる電圧を求めることができます。 これを分圧の式と呼ぶことがあります。

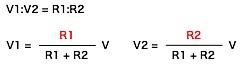
並列回路と並列接続

２つの抵抗を接続した回路を考える場合、下の図ような回路を並列回路と呼び、 このような抵抗の接続方法を並列接続と呼んでいます。

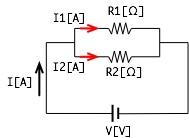
並列回路の特徴としては、各抵抗に加わる電圧は一定（同じ）で、電流は各抵抗にて分配されます。 これを分流と言います。つまり、以下の関係式が成立します。

I = I1 + I2・・・(5)
I1= V／R1  ・・・(6)
I2= V／R2  ・・・(7)

次に直列回路と同様の等価回路を考え、合成抵抗を求めてみます。

I = V／R ・・・(8)

(6)、(7)、(8)式を(5)式へ代入します。

V／R = V／R1 + I2= V／R2

両辺からVを消去して、

1／R = 1／R1 + 1／R2

ゆえに、

R = 1／(1／R1 + 1／R2)

並列接続の合成抵抗は、合成抵抗の逆数が、各抵抗値の逆数の総和となります。 そのため合成抵抗はさらにその逆数となるので、ちょっと注意が必要です。 ただ、抵抗が２つの場合は、以下の式で求めることができます。

R = (R1・R2)／(R1 + R2)  これは和分の積と覚えます。

また、並列接続されている抵抗値が同じ場合は、その抵抗値を抵抗の個数で割ったものが合成抵抗になります。

R = r／n 同一抵抗値r を n個並列接続の場合

直列接続では分圧により電圧を計算しましたが、並列接続では、電圧考えることなく各抵抗にかかる電流を求めることができます。 これを分流の式と呼ぶことがあります。

先頭に戻る