2. 波の基本
正弦波
波にもいろんな波があります。最も基本となる形の波を正弦波と言います。 また、波を伝える物質のことを媒質と呼びます。我々が扱う音の場合、その媒質は空気になります。
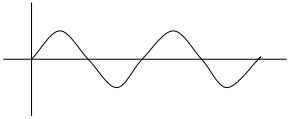
波長
波長とは波の長さのことで、通常、記号λで表し、単位は[m]になります。また、波は同じ形が繰り返し現れるので、 その波の形ひとつ分の長さを、1波長と呼びます。この1波長は山から山の長さになりますが、 場所をどの位置にしても、波長は変化しません。
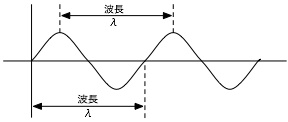
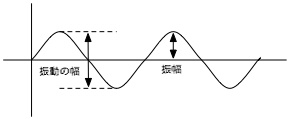
振幅
振幅とは、波の振れ幅のことで、通常、記号Aで表し、単位は[m]になります。 波の振れの一番低い点と一番高い点の差を振動の幅と呼ぶこともありますが、 その振動の幅の半分の長さを振幅と言います。
速さ
波にも速さがあります。通常、記号Vで表し、単位は[m/s]になります。
周波数
ある点が1秒間に振動する回数を振動数あるいは周波数と呼びます。 通常、記号fで表し、単位は[Hz]になります。 以下のグラフは、ある点が時間=0のとき原点位置で、時間が0.25経過すると最高に達し、 順次状態が変化したものをグラフ化したものです。 つまり、1周期の形を描き終わるまでを1回の振動と数えています。 下のグラフでは、丁度1秒で1回の振動なので、振動数は1、要するに周波数は1[Hz]ということになります。
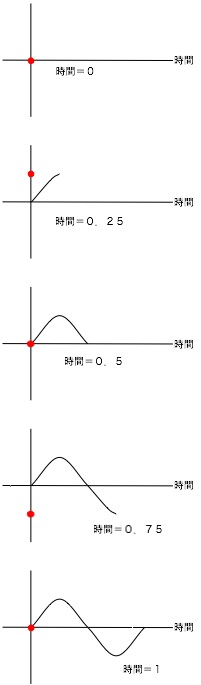
また、振動数の逆数で「1回振動するのに何秒かかるか」という量を周期と言います。 通常、記号Tで表し、単位は[s]になります。
波長・振幅・速さ・周波数の関係
この波長、振幅、速さ、周波数には、それぞれ関係を持っています。例えば、以下の図で、時間が1秒のときを考えてみます。
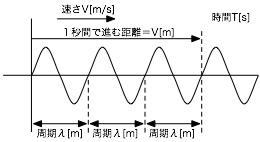
この図の場合、1秒間に波長λ[m]の波が3回あるとすると、周波数は3[Hz]ということになります。 また、1秒間に進む距離はV[m]ですから、
V[m] = λ[m] ・ f[Hz]
となります。また、周期T[s]は、1秒間に3回ですから、1/3[s]が1周期の時間となります。これを式で表すと、
T[s] = 1 / f[Hz]
となります。この2つの式を合わせると、
V[m/s] = λ[m] ・ f[Hz] = λ[m] / T[s]
となります。つまり、
λ[m] = V[m/s] / f[Hz]
となります。これらの関係式はとても大事なのでよく覚えておきましょう。
位相
位相とは、波の中での位置を表すものです。下のグラフでは、半径1の円周上の赤点の運動を正弦波で表現したものです。 角度が0度のとき原点位置となり、点bでは角度90度、点cでは角度180度、点dは角度270度、再び点aに戻ると角度360度となり、 この角度が位置を表現しています。これも位相となります。なお、グラフでは、位相をラジアンで表現しています。
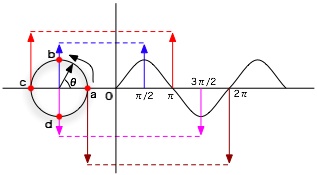
次に、この位相を使って2つの波の関係を見てみます。まず、最初の図では、 波Bが波Aよりも360度進んでいる形の波で、波の形自体は同じです。 このような波Bを波Aに対して正位相(正相)であると言います。
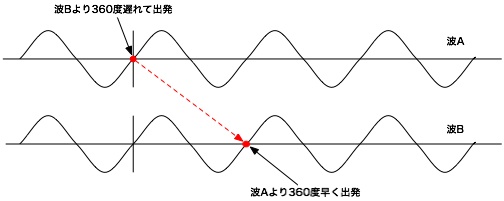
2つ目の図は、波Bが波Aよりも180度進んでいる形の波で、波Aに対して波Bが丁度反対になった形になります。 このような波Bを波Aに対して逆位相(逆相)であると言います。
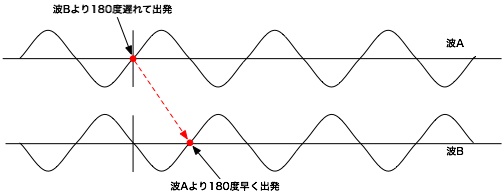
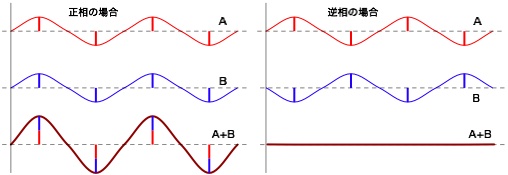
2つ以上の波が重なるとある位相における波は、その和となります。つまり、正相の場合は、振幅が2倍になります。 反対に逆相の場合は、お互いが打ち消し合うので、振幅が0となります。 音では、この正相と逆相はとても大事です。例えば、ステレオの音をモノラルで聴く場合、LチャンネルとRチャンネルの和を聴くことになるので、 逆相の場合、センタに定位されている音は打ち消し合い、聞こえないという現象が発生します。
平面波と球面波
これまでは波を真横から見た感じの図ばかりだったが、それを立体的に見ると、次のようになる。
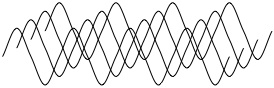
ここで波の山同士(谷同士でもいい)を線でつなげると下の図のようになる。 こうしてできた線の部分を波面と呼ぶ。
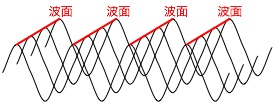
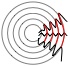
このように波面が直線、または平面となる場合の波を平面波と言います。 また、波の元からの波面が球面上になるものを球面波と呼びます。
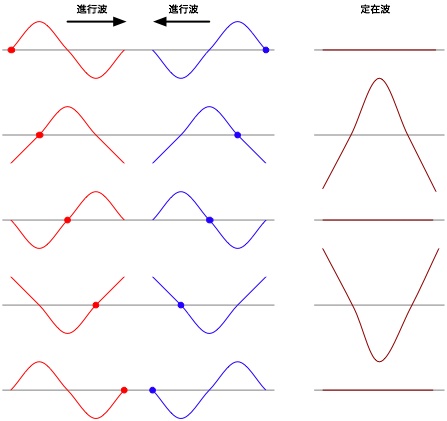
進行波と定在波
これまで見てきた波は、ある速度を持ち、進む方向を持った波です。このような波を進行波と呼びます。 これに対して、波の進行が止まったように見え、振幅が同じ場所で繰り返されるような波があります。これを定在波と呼びます。 下の図は、2つの進行方向が反対向きの波の合成(干渉と言います。)によって、定在波ができる様子を表しています。